A paper entitled "Minimum Label s-t Cut has large integrality gaps" was recently published in IANDC (Information and Computation), a top journal in the field of theoretical computer science, with Associate Professor Zhang Peng from School of Software being the first author and corresponding author.The paper reveals the computational hardness of the Label Cut problem. Shandong University is the first author institution of this paper, and Institute of Software, Chinese Academy of Sciences is the cooperation organization.
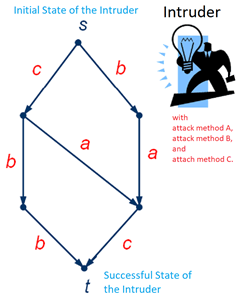
The Label s-t Cut problem is a typical combinatorial optimization problem arising in several areas such as system security and computer network. In the area of system security, the attack to the system by the intruder can be expressed by a directed graph. At the beginning, the intruder with some attach methods is in his initial state named s. If the intruder reaches the success state named t, it means that the intruder has successfully intruded into the system. If the intruder applies an attack method from one state, his state will be changed into another state. Therefore, the task of the defender of the system is to destroy (or disable) some attack methods of the intruder at the minimum cost, so that the intruder cannot reach the successful state. A labeled directed graph will be obtained if one uses vertices to represent the states, directed edges to represent the transitions of states, and labels to represent the attack methods. In this way, the task of the defender can be restated as finding a minimum cost set of labels, such that the removal of edges having these labels from the graph would disconnect vertex s and vertex t. This is exactly the Label s-t Cut problem. It is easy to see that this problem is a generalization of the classic Min s-t Cut problem.
The Label s-t Cut problem has already been proved to be NP-hard. Consequently, it is natural to approximately solve this problem by approximation algorithms. The linear programming technique is so powerful in the design of approximation algorithms for NP-hard problems that it has been applied widely and extensively. Using the probabilistic method, Zhang Peng with his cooperator proved that, the integrality gap of a natural linear program for Label s-t Cut is at least Omega(m1/3), where m is the number of edges in the input graph. This result shows that desired approximation ratio for Label s-t Cut cannot be strictly better than O(m1/3), if one designs approximation algorithms for the problem by using pure linear programming techniques. This reveals the high computational hardness of the Label s-t Cut problem.

IANDC is a top journal of class A in the field of theoretical computer science authorized by China Computer Federation. In tradition, theoretical computer science is a branch of mathematics filled with deep research problems. The research in this filed usually faces high difficulties, and the paper reviewing in this field often has a long period. IANDC publishes less than one hundred papers in average per year. Among those, the papers coming from China are actually very rare. Organizations from China only published three papers in IANDC in 2018, and four papers in 2019, with authors of these papers coming from several famous universities and research organizations in China such as Shanghai Jiao Tong University, Nanjing University, and Institute of Software, Chinese Academy of Sciences. The paper in IANDC by Zhang Peng et al. is the first CCF-A paper in theoretical computer science published by School of Software, Shandong University. This research was supported by the National Natural Science Foundation of China, the Natural Science Foundation of Shandong Province, and the Fundamental Research Funds of Shandong University.
Paper link:
https://www.sciencedirect.com/science/article/pii/S0890540120300316
Written by: Zhang Peng
Edited by: Che Huiqing